简介
为了应付高代考试,浅浅复习(学习)并整理了一下。
参考教材为《高等代数学》(第四版)--谢启鸿
内容为第五章到第八章内容
1 第五章
1.1 Vieta定理
韦达定理描述多项式的根与系数之间的关系
对于n次多项式 f(x) = x^n + a₁x^(n-1) + a₂x^(n-2) + ... + aₙ
设其n个根为x₁, x₂, ..., xₙ,则:
x₁ + x₂ + ... + xₙ = -a₁ (根的和)
x₁x₂ + x₁x₃ + ... + xₙ₋₁xₙ = a₂ (根的两两乘积之和)
x₁x₂x₃ + ... = -a₃ (根的三三乘积之和) ... n. x₁x₂...xₙ = (-1)^n·aₙ (所有根的乘积)
例如:对于二次方程 x² + px + q = 0 设两根为x₁, x₂ 则: x₁ + x₂ = -p x₁x₂ = q
对于三次方程 x³ + ax² + bx + c = 0 设三根为x₁, x₂, x₃ 则: x₁ + x₂ + x₃ = -a x₁x₂ + x₁x₃ + x₂x₃ = b x₁x₂x₃ = -c
1.2 Eisenstein判别法
Eisenstein判别法用于判断一个多项式是否是不可约多项式
设f(x)=aₙxⁿ+aₙ₋₁xⁿ⁻¹+...+a₁x+a₀是整系数多项式,如果存在一个素数p满足:
p不整除最高次项系数aₙ
p整除所有其他项系数(aₙ₋₁,aₙ₋₂,...,a₁,a₀)
p²不整除常数项a₀
则f(x)在有理数域上不可约。
例如:判断f(x)=x³+6x²+12x+18是否不可约
取p=3
检查:
3不整除1(最高次项系数)
3整除6,12,18(其他项系数)
3²=9不整除18(常数项)
满足所有条件,所以f(x)在有理数域上不可约
注意事项:
Eisenstein判别法是充分不必要条件
如果直接使用不成功,可以尝试:
替换x为x+k(k为整数)
替换x为kx(k为整数)
不能判定的多项式不一定是可约的
这个判别法在代数学中很有用,特别是在判断多项式不可约性时。
1.3 结式与判别式
结式(Resultant)是判断两个多项式是否有公共根的重要工具
定义: 对于两个多项式 f(x)=aₙxⁿ+aₙ₋₁xⁿ⁻¹+...+a₁x+a₀ g(x)=bₘxᵐ+bₘ₋₁xᵐ⁻¹+...+b₁x+b₀
结式可以通过以下方式求得:
Sylvester矩阵法:
构建(m+n)×(m+n)的Sylvester矩阵
结式R(f,g)等于Sylvester矩阵的行列式
基本性质:
如果f(x)和g(x)有公共根,则R(f,g)=0
如果R(f,g)=0,则f(x)和g(x)有公共根
R(f,g)可以表示为f(x)和g(x)系数的多项式
例如: f(x)=ax²+bx+c g(x)=px+q 结式为: |a b c 0| |0 a b c| |p q 0 0| |0 p q 0|
应用:
判断多项式是否有公共根
消去方程组中的变量
判断曲线是否相交
注意:
结式为0是两个多项式有公共根的充要条件
计算高次多项式的结式可能很复杂
结式的性质在代数几何中有重要应用
1.4 做题知识点
首一多项式:最高项系数为1的多项式
deg:多项式的最高次数
f(x)是数域 F 上的多项式,且 K 是包含 F 的数域,若f(x)在K上不可约,则f(x)在F上不可约
f(x)是实数域上的多项式,若 p_1(x),p_2(x)是f(x)的不可约因式,且 p_1(x),p_2(x)在有理数域内互素,则 p_1(x),p_2(x)在复数域内无公根
对称多项式:各元素交换后结果不变
例如
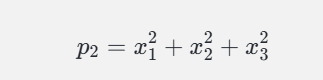
2 第六章
2.0 几种矩阵间关系(略微复习)
2.0.1 可逆矩阵
B=A^-
AB=BA=E
判定条件(以下条件等价):
det(A)≠0(行列式不为零)
矩阵的秩等于阶数
齐次方程组AX=0仅有零解
矩阵A的行(列)向量线性无关
0不是矩阵A的特征值
特征多项式的常数项不等于0
2.0.2 转置矩阵
如果 A 是一个 m×n 的矩阵
那么 A 的转置矩阵 AT 是一个 n×m 的矩阵
AT 中的每个元素 (AT)ij = Aji
转置的性质:(AT)T = A(转置的转置等于原矩阵)
2.0.3 数量矩阵
是一个方阵(行数等于列数)
主对角线上的所有元素都相等
非主对角线上的元素都为0
2.0.4 伴随矩阵
AA* = A*A = |A|I
2.1 特征值
对于任意实数k,|A + kI₃| = (λ₁ + k)(λ₂ + k)(λ₃ + k)
几种矩阵的特征值与原矩阵特征值关系
逆矩阵特征值为原矩阵特征值的倒数
与原矩阵具有相同的特征值
矩阵特征值为λ,其伴随矩阵的特征值为λⁿ⁻¹
转置矩阵特征值与原矩阵相同
2.2 特征向量
2.3 特征矩阵
λ In-A
2.4 特征多项式
|λ In-A |

2.5 矩阵对角化
2.5.1 可对角化矩阵定义
设 A 是 n 阶矩阵,若 A 相似于对角阵,即存在可逆矩阵 P,使 P^{-1}AP 为对角阵,则称 A 为可对角化矩阵
2.5.2 可对角化的充要条件
设 A 是 n 阶矩阵,则 A 的可对角化的充要条件是 A 有 n 个线性无关的特征向量
2.6 相似矩阵
相似矩阵具有相同极小多项式
2.7 Cayley-Hamilton定理
设 A 是数域 K 上的 n 阶矩阵, f(x) 是 A 的特征多项式,则 f(A) = O
2.8 极小多项式
若 n 阶矩阵 A (或 n 维线性空间 V 上的线性变换 φ )适合一个非零首一多项式 m(x) ,且 m(x) 是 A (或 φ )所适合的非零多项式中次数最小者,则称 m(x) 是 A (或 φ )的一个极小多项式或最小多项式
2.9 做题知识点
当 n 阶矩阵 A 有 n 个不同的特征值(有 n 个线性无关的特征向量)时,它必相似于对角矩阵
n 阶矩阵 A 以任一 n 维非零列向量为特征向量的充要条件是 为数量矩阵
属于不同特征值的特征向量必线性无关,属于同一特征值的特征向量也不一定线性相关
相似矩阵必有相同的特征值,特征值相同的矩阵未必相似
若矩阵 A 只和自己相似,则矩阵必为数量矩阵
3 第七章
3.0 相似矩阵
3.0.1 性质
两者的秩相等
两者的行列式值相等
两者的迹数相等
两者拥有同样的特征值,尽管相应的特征向量一般不同
两者拥有同样的特征多项式
两者拥有同样的初等因子
A 和 A^T 相似
3.1 多项式矩阵
3.1.1 \lambda -矩阵
3.1.2 \lambda -矩阵的初等变换
将A(λ) 的两行对换
将 A(λ) 的第 i 行乘以 K 中的非零常数 c
将 A(λ) 的第 i 行乘以 K 上的多项式 f(λ) 后加到第 j 行上去
3.1.2.1 第三类初等矩阵

对\lambda -矩阵 A(λ) 施行第 k(k= 1,2,3)类初等行(列)变换等于用第k 类初等\lambda -矩阵左(右)乘以A(λ)
3.1.2.2 可逆阵


3.2 矩阵的法式(相抵标准型)
在线性代数中,相抵标准型是指矩阵在相抵关系下的一种标准形式。对于给定的矩阵,通过一系列初等行变换和初等列变换,可以将其化为一个相对简单的形式。对于矩阵 A,如果存在可逆矩阵 P 和 Q,使得 PAQ化为相抵标准型,则称 A 与其相抵。

3.2.1 求解方式
找最小非零元素:
将最小非零元素通过行列变换移到左上角(1,1)位置
消元:
用(1,1)位置元素消去第一行和第一列其他元素
重复操作直到无法继续消元
处理子矩阵:
对剩余子矩阵重复上述步骤
直到得到对角矩阵
检查整除关系:
确保对角线上的元素满足整除关系
如果不满足,需要进行调整
3.3 不变因子
3.3.1 行列式因子

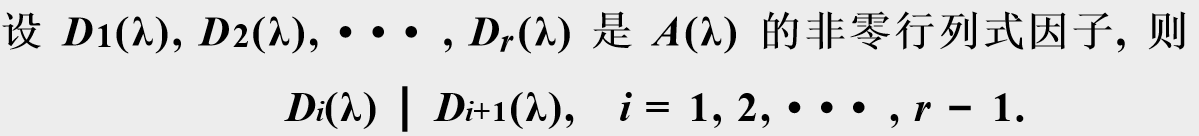
3.3.2 不变因子定义


3.3.3 与法式关系





3.4 有理标准型




3.4.1 定义

3.4.2 极小多项式


3.4.3 根据矩阵求有理标准型
求出矩阵的相抵标准型
根据相抵标准型求出行列式因子
根据行列式因子求出不变因子
确定有理标准型矩阵阶数,为不变因子组个数
次对角线为1,最后一行为p(λ)系数的相反数


3.5 初等因子
3.5.1 定义


由因式分解的唯一性可知 A 的初等因子被 A 的不变因子唯一确定
3.5.2 与矩阵相似的关系

3.5.3 根据不变因子组求初等因子组
先从不变因子组中找出所有不同的因式(如λ、λ-1等)
对每个因式:
写出它在每个不变因子中的指数序列(从高次到低次排列)
计算相邻指数的差(指数差)
根据指数差和最高指数确定初等因子
具体规则:
指数差表示在该级别上需要的初等因子的个数
最后一个非零指数决定最高次幂
按照指数从低到高写出初等因子
例如:某因式在不变因子中的指数序列是3,2,1
指数差:3-2=1, 2-1=1
指数差为1,1表示每级都需要1个因子
最高指数为3
所以初等因子为:λ,λ²,λ³
3.5.4 根据初等因子组求不变因子组
确定不变因子组个数,即矩阵阶数,每个初等因子的阶数之和即为所求
从后往前确定不变因子
其余都补1
重要性质:
不变因子个数=矩阵阶数
后面的不变因子可以整除前面的不变因子
所有不变因子的乘积=所有初等因子的乘积
最前面的若干个不变因子一定都是1
3.6 Jordan标准型
3.6.1 重要引理




3.6.2 定义


3.6.3 相关推论





3.6.4 求解方法
求出初等因子
填充
对于k阶Jordan块的标准形式是:
|λ 1 0 ... 0|
|0 λ 1 ... 0|
|0 0 λ ... 0|
|. . . . .|
|0 0 0 ... λ|其中:
λ是特征值
主对角线上全是λ
主对角线上方的次对角线填1
其他所有位置都是0
3.7 做题知识点
矩阵初等因子个数为 jordan 标准型 jordan 块的个数,每个初等因子的次数即为该 jordan 块矩阵阶数
第三类初等多项式矩阵不可对角化
非零幂零矩阵,即A^k = 0,不相似于对角矩阵(不可对角化)
极小多项式(最后一个不变因子)不为0,矩阵必可逆
不变因子组乘积即为特征多项式
若矩阵某特征值为0,矩阵不可逆(为奇异阵)
4 第八章
4.1 矩阵的合同
4.1.1 定义

4.1.2 其他性质
正特征值个数相等,负特征值个数相等
秩相同
合同矩阵的行列式同号或互为相反数
4.2 二次型
4.2.1 定义
二次齐次多项式
4.2.2 特征
每一项都是二次方
4.2.3 矩阵表示
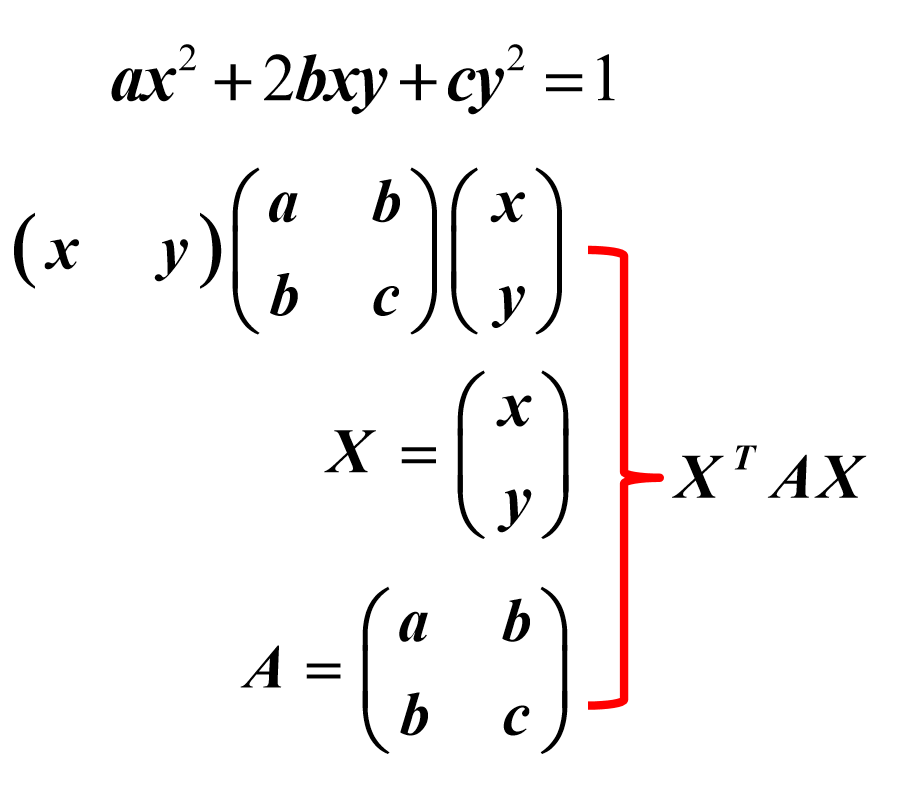
其中 A 就是二次型的矩阵
二次型的矩阵都是对称矩阵

4.2.4 二次型的标准型
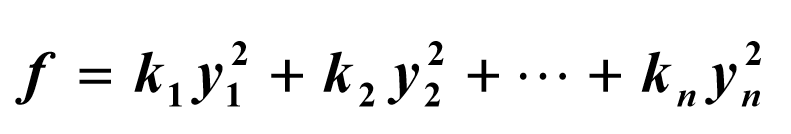
4.2.5 与标准型进行转换
4.2.5.1 正交变换法
步骤:
写出矩阵
求特征值
求特征向量
构造正交矩阵
得到标准型
例如:2x² + 2y² + 2xy
矩阵形式: [2 1] [1 2]
求特征值: |2-λ 1 | = 0 |1 2-λ| 得到: λ₁=3, λ₂=1
求特征向量,构造正交矩阵P 最终标准型为: 3u² + v² 其中u,v是新变量
4.2.5.2 配方法
例如: x² + 4xy + 4y²
先对x配方: (x² + 4xy) + 4y² = (x + 2y)² + 4y² - 4y²
最终得到: (x + 2y)²
4.2.6 二次型的化简



4.3 惯性定理

正惯性系数即为正特征值个数,负惯性系数为负特征值个数

4.4 正定型与正定矩阵
4.4.1 重要定理及推论
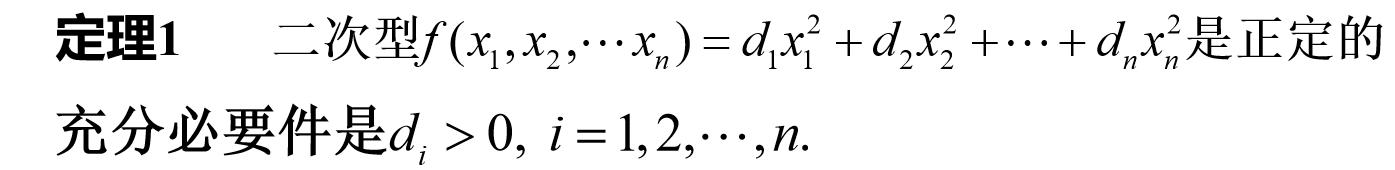
可逆线性变换不改变二次型的正定型

实对称矩阵 A 正定的充要条件是 A 合同于单位矩阵
实对称矩阵 A 的充要条件是 A 的特征值全部为正值
正定矩阵的行列式大于0
设 A 是实对称矩阵,则 A 正定的充要条件是其顺序主子式均大于0

4.4.2 判定
定义法
对于任意非零向量X,如果二次型f(X) > 0,则为正定
即对所有非零的(x₁,x₂,...,xₙ),都有f(x₁,x₂,...,xₙ) > 0
特征值法
计算矩阵的所有特征值
如果所有特征值都大于0,则为正定
如果有特征值≤0,则不是正定
顺序主子式法(最常用)
计算矩阵的各阶顺序主子式
如果所有顺序主子式都大于0,则为正定 例如对于3阶矩阵:
|a₁₁| > 0
|a₁₁ a₁₂|
|a₂₁ a₂₂| > 0
|a₁₁ a₁₂ a₁₃|
|a₂₁ a₂₂ a₂₃| > 0
|a₃₁ a₃₂ a₃₃|4.5 做题知识点
若 A 是 n 阶实反对称矩阵,则AA^T必是半正定阵,当A可逆时,AA^T必是正定阵
设可逆矩阵 A 和 B 合同,问A^-和B^-合同
任意两个同阶正定阵合同(都合同于单位阵)
矩阵是正定阵,其伴随矩阵也是正定阵
设 A 是正定阵,A^k(k>1)也是正定阵
矩阵特征值为0,不是正定阵
设 n 阶实对称矩阵 A , B 都是正定阵,\left( \begin{matrix} A & 0\\ 0 & B \end{matrix} \right) \tag{2} 也是正定阵




评论区